Merge Sort
2018, Jul 11
Merge Sort 에 대해 알아보자. Time Complexity 는 O(nlogn) 이다.
Merge Sort 진행과정은 이렇다. 주어진 배열을 반으로 계속 나눈 뒤, 나눈 배열을 비교하여 정렬하고 다시 합친다.
여기에 대한 이해를 돕는 아래 그림은 https://www.geeksforgeeks.org/merge-sort 에서 참고했다.
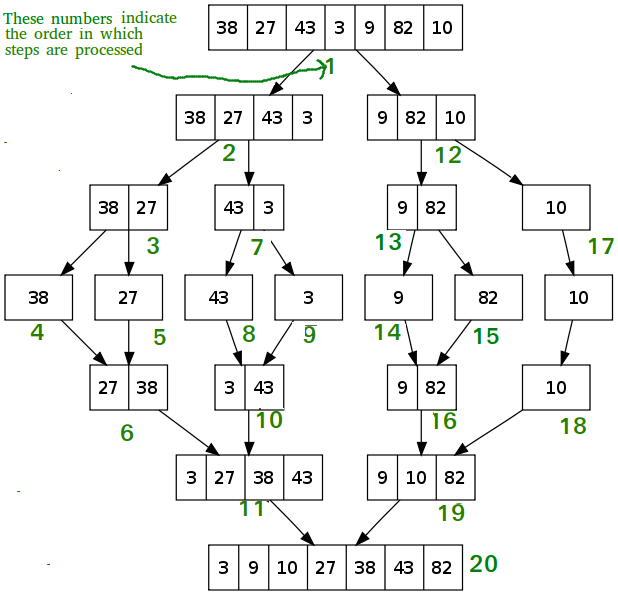
먼저 메인 함수부터 보며 시작해보자. 배열 사이즈를 사용자로부터 입력받고, 사이즈만큼 배열 요소를 입력받는다.
#include <stdlib.h>
#include <stdio.h>
int main()
{
// 받게될 배열 사이즈이다.
int size; scanf("%d",&size);
// 사이즈 만큼 배열을 선언한다.
int* arr = (int*)malloc(sizeof(int)*size);
// 정렬해야할 배열요소를 입력받는다.
for(int i=0; i<size; i++)
scanf("%d",&arr[i]);
// Merge Sort 시행한다.
mergeSort(int* arr, int left, int right);
// 정렬한 배열을 출력한다.
for(int i=0; i<size; i++)
printf("%d ", arr[i]);
printf("\n");
free(arr);
}Merge Sort 기능을 구현해보자.
void mergeSort(int* arr, int left, int right)
{
// 쪼갠 배열의 size 가 1이하이면 종료한다.
if(left >= right) return;
// 인자 배열을 반으로 쪼갠다.
int middle = (left+right) / 2;
mergeSort(arr, left, middle);
mergeSort(arr, middle+1, right);
// 쪼갠 배열을 정렬하고 병합한다.
// 임시 배열을 이용한다.
// 임시 배열 사이즈
int n1 = middle-left+1;
int n2 = right-middle;
int* tArr1 = (int*)malloc(sizeof(int)*n1);
int* tArr2 = (int*)malloc(sizeof(int)*n2);
memcpy(tArr1,&arr[left],sizeof(int)*n1);
memcpy(tArr2,&arr[middle+1],sizeof(int)*n2);
// 임시배열을 비교하며 정렬한다.
int leftCnt=0; int rightCnt=0;
int arrIndex = left;
while(leftCnt < n1 && rightCnt < n2)
{
if(tArr1[leftCnt] < tArr2[rightCnt])
{
arr[arrIndex] = tArr1[leftCnt];
leftCnt++;
}
else
{
arr[arrIndex] = tArr2[rightCnt];
rightCnt++;
}
arrIndex++;
}
// 남은 임시배열 요소를 정렬된 배열 뒤에 붙여준다.
while( leftCnt < n1 )
{
arr[arrIndex] = tArr1[leftCnt];
leftCnt++;
arrIndex++;
}
while( rightCnt < n2 )
{
arr[arrIndex] = tArr2[rightCnt];
rightCnt++;
arrIndex++;
}
free(tArr1); free(tArr2);
}적절하게 mergeSort 를 호출하면 정렬이 되는 것을 확인할 수 있다!!