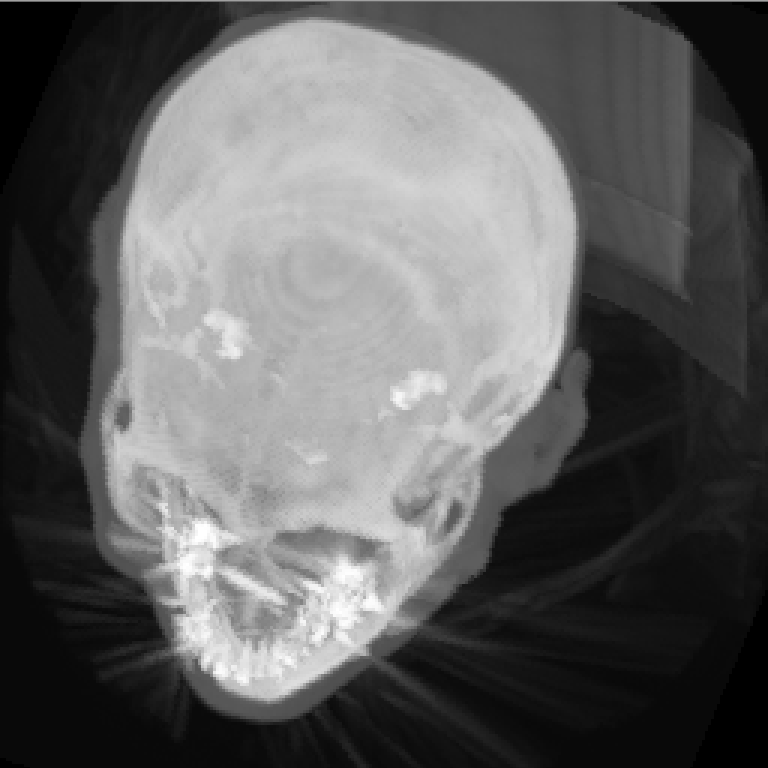
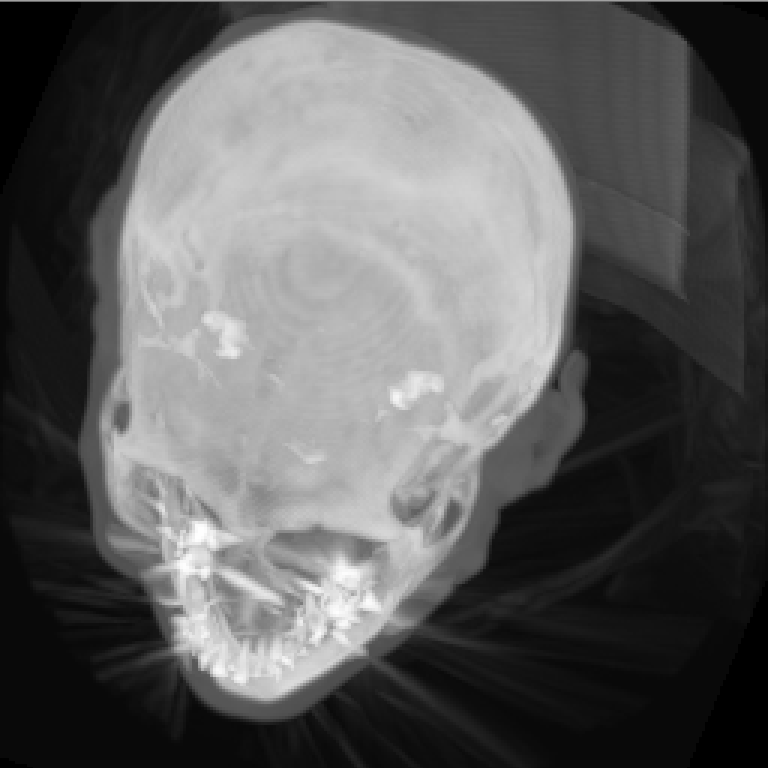
실수 좌표의 voxel 값을 가져오는 기능을 만들어보자.
기존의 GetVoxel 함수를 보면 이렇다.
Volume.cpp
unsigned char GetVoxel(int x, int y, int z)
{
return m_volume.get()[width*height*z + width*y + x];
}함수의 인자로 정수형을 받기 때문에 실수를 입력하면 버림 연산된다. 따라서 입력 좌표의 근처 정수 좌표의 voxel 값이 return 된다. 이는 이미지 내에 계단현상이 일어나는 원인이 될 수 있다.
실수형 좌표에 해당하는 voxel 값을 return 하려면 입력 좌표와 근처 좌표들 사이의 거리를 구하여 가중평균하여야 한다. 다시 말하자면,
- 근처 정수 좌표 voxel 값을 구한다.
- 거리에 반비례하는 가중치를 voxel에 곱하고 더한다.
1차원에서 직선에서 보자면 점(0)과 점(1) 사이의 좌표(0.7) voxel 값을 구한다고 했을 때,
위치 0 voxel 120
위치 1 voxel 150 이라면
120 X (1-0.7) + 150 X 0.7 이다.
이를 2차원 평면으로 확대하면, 좌표 a(0,0), 좌표 b(1,0), 좌표 c(0,1), 좌표 d(1,1) 사이의 r(0.7, 0.4) voxel 값을 구한다고 했을 때,
위치 c voxel 130 위치 d voxel 225
위치 a voxel 120 위치 b voxel 150 이라면
직선 ab 의 0.7 위치의 voxel 값은 120 X (1-0.7) + 150 X (0.7) 직선 cd 의 0.7 위치의 voxel 값은 130 X (1-0.7) + 225 X (0.7)
이렇게 만들어진 두 점 e, f를 이은 직선을 ef 라고 했을 때,
위치 e voxel 120 X (1-0.7) + 150 X (0.7)
위치 f voxel 130 X (1-0.7) + 225 X (0.7) 이고
직선 ef 의 0.4 위치의 voxel 값은 위치 e 의 voxel X (1-0.4) + 위치 f 의 voxel X (0.4) 이다.
마찬가지로 3차원 평면으로 확대하면, 2차원에서 구한 좌표의 voxel 값을 a, 맞은 편 평면의 좌표에서의 voxel 값을 b, 라고 하면
3차원 voxel 값은 = a X 가중치 + b X 가중치 가 된다.
이를 코드로 구현해보자.
Volume.cpp
float Volume::GetVoxel(float x, float y, float z)
{
// tri - linear interpolation
int x_minus = x;
int y_minus = y;
int z_minus = z;
int x_plus = x + 1;
int y_plus = y + 1;
int z_plus = z + 1;
float x_weight = x - static_cast<float>(x_minus);
float y_weight = y - static_cast<float>(y_minus);
float z_weight = z - static_cast<float>(z_minus);
unsigned char coord_000 = GetVoxel(x_minus, y_minus, z_minus);
unsigned char coord_100 = GetVoxel(x_plus, y_minus, z_minus);
unsigned char coord_010 = GetVoxel(x_minus, y_plus, z_minus);
unsigned char coord_110 = GetVoxel(x_plus, y_plus, z_minus);
unsigned char coord_001 = GetVoxel(x_minus, y_minus, z_plus);
unsigned char coord_101 = GetVoxel(x_plus, y_minus, z_plus);
unsigned char coord_011 = GetVoxel(x_minus, y_plus, z_plus);
unsigned char coord_111 = GetVoxel(x_plus, y_plus, z_plus);
float res_000_100 = coord_000 * (1.f - x_weight) + coord_100 * x_weight;
float res_010_110 = coord_010 * (1.f - x_weight) + coord_110 * x_weight;
float res_2d_1 = res_000_100 * (1.f - y_weight) + res_010_110 * y_weight;
float res_001_101 = coord_001 * (1.f - x_weight) + coord_101 * x_weight;
float res_011_111 = coord_011 * (1.f - x_weight) + coord_111 * x_weight;
float res_2d_2 = res_001_101 * (1.f - y_weight) + res_011_111 * y_weight;
float res = res_2d_1 * (1.f - z_weight) + res_2d_2 * z_weight;
return res;
}위의 코드는 입력 받은 좌표의 +1 의 좌표에 접근하기 때문에 Renderer 에서 수정사항이 발생한다.
범위를 하나 줄여줘야 한다.
Renderer.cpp
bool Renderer::RenderMIPAnyDirection(unsigned char* image,
const int img_width, const int img_height)
{
...
/// 아래 범위체크에서 체크 범위를 하나 줄인다.
if (cur_coord.x >= 0.f && cur_coord.x < vol_width-1 &&
cur_coord.y >= 0.f && cur_coord.y < vol_height-1 &&
cur_coord.z >= 0.f && cur_coord.z < vol_depth-1)
{
///해당 위치에서의 볼륨 복셀을 가져옴
float voxel =
m_pVolume->GetVoxel(cur_coord.x, cur_coord.y, cur_coord.z
///맥스값 비교
max_value = __max(max_value, voxel);
}
...
}결과는 다음과 같다.
위는 기능을 적용하지 않았을 때 결과이고
아래는 적용한 결과이다. 계단 현상이 많이 감소했음을 알 수 있다.